Example: Using Graph Kernels for Feature Generation

This example shows how to use graph kernels for feature generation. The corresponding RapidMiner workflow can be downloaded from myExperiment.

The RapidMiner LOD extension integrates two types of graph kernels for RDF data from the mustard library:

1. RDF Walk Count Kernel: This kernel counts the different walks in the subgraphs (upto the provided Graph Depth) around the instances nodes. The maximum length of the walks to consider is given by the Walk Length parameter.

• (Fast) This is a fast approximation of counting all the walks in the subgraph, which is done with the Full setting.
• (Root) Only consider walks that start with the instance node (i.e. the root).
• (Tree) Count all the walks in the subtree that is rooted in the instance node. This is faster than the Full subgraph version, since a tree does not contain cycles.
• (Full) Count all the walks in the subgraph. NOTE, this variant is typically very slow.

2. RDF WL Sub Tree Kernel: This kernel counts the different full subtrees in the subgraphs (upto the provided Graph Depth) around the instances nodes, using the Weisfeiler-Lehman algorithm. The maximum size of the subtrees is controlled by the number of iterations parameter.

• (Fast) This is a fast approximation of counting all the subtrees in the subgraph, which is done with the Full setting.
• (Root) Only consider subtrees that start with the instance node (i.e. the root). NOTE, this setting is included for completeness, it will likely give very bad results.
• (Tree) Count all the subtrees in the subtree that is rooted in the instance node. This is faster than the Full subgraph version, since a tree does not contain cycles.
•  Full) Count all the subtrees in the subgraph.

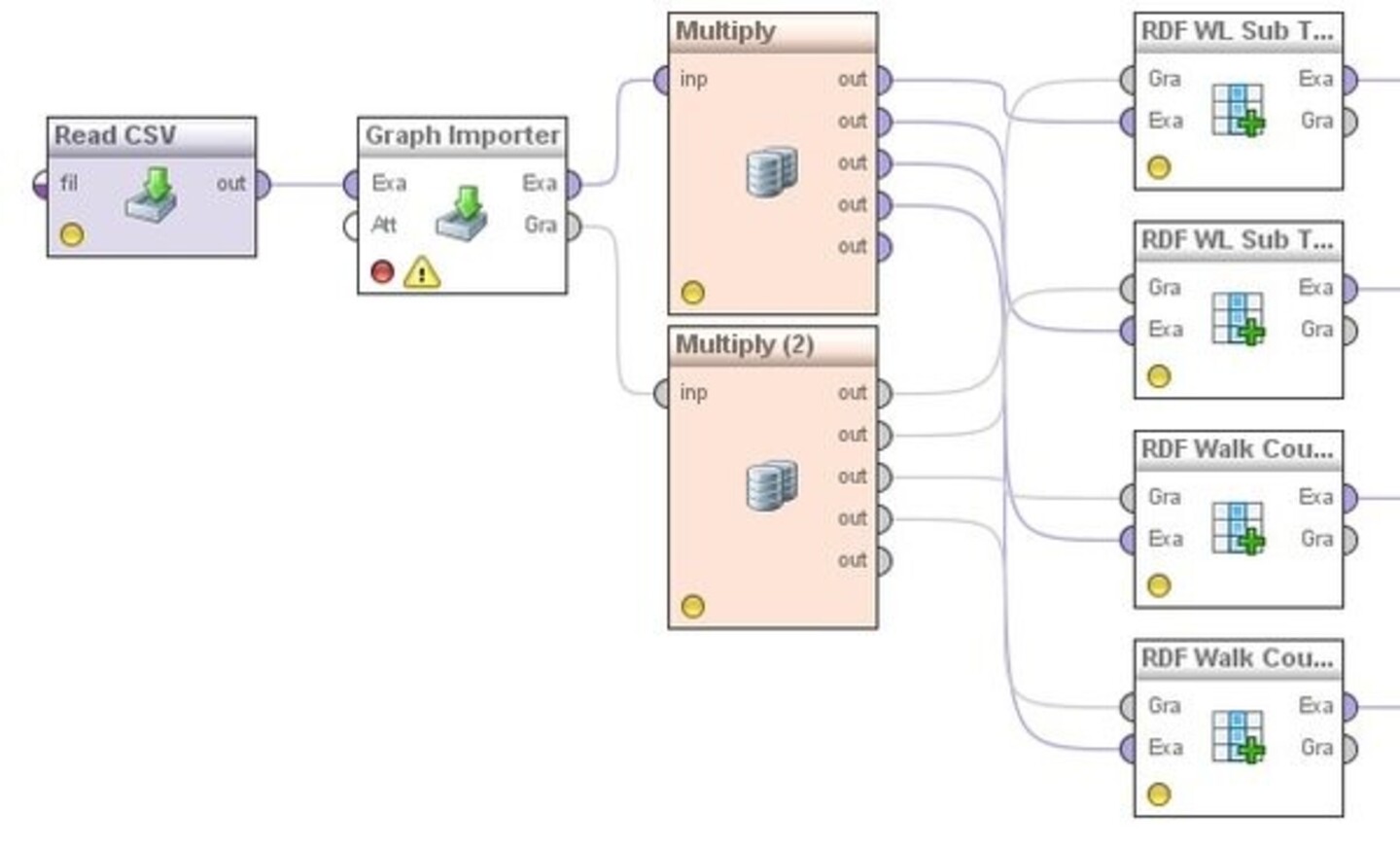
In this example we use the Root RDF Walk Count Kernel [1], and the Fast RDF WL Sub Tree Kernel [2]. The process (see figure below) starts with reading a CSV file. The file contains a list of French regions with unemployment rate as a label, including a DBpeida URI for each region (get the dataset here).

Next, we use the “Graph Importer” operator to import a sub-graph from DBpedia for the French regions. To do so, we use the DBpedia endpoint, we select  “DBpedia_URI” attribute to be extended, we select graph depth of 2, and we add the regular expression “http://dbpedia.org/property.*" in the parameter “Properties to be avoid” in order to avoid the “dbprop” namespace properties.

Then, we connect the graph output of the “Graph Imporeter” operator to the graph input port of the Kernel operators. We do the same for the ExampleSet. We use four graph kernel operators: (i) Root RDF Walk Count Kernel with walk lenghth 2, (ii) Root RDF Walk Count Kernel with walk length 3, (iii) Fast RDF WL Sub Tree Kernel with graph depth 1 and 2 iterations, (iv) Fast RDF WL Sub Tree Kernel with graph dept 2 and 2 iterations.